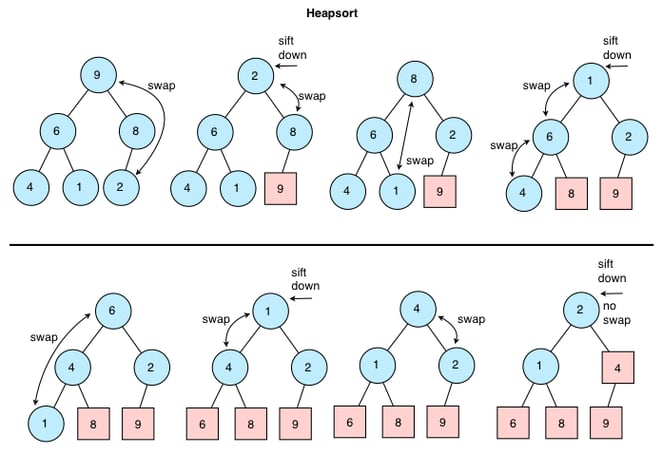
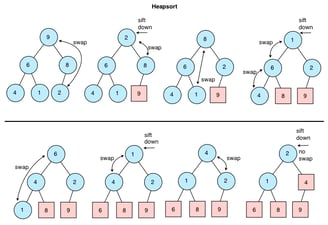
And that’s basically it! The algorithm continues to repeat these steps until the heap is down to just one single node. At that point, it knows that all the elements in the unsorted array are in their sorted positions and that the last node remaining will end up being the first element in the sorted array. The total running time of this algorithm is O(n log n).

Merge Sort

The merge sort algorithm is a sorting algorithm that sorts a collection by breaking it into halves. It then sorts those two halves, and then merges them together, in order to form one, completely sorted collection. In most implementations of merge sort, it does all of this using recursion.

Merge sort is a divide and conquer algorithm which can be boiled down to 3 steps:

Divide and break up the problem into the smallest possible “subproblem”, of the exact same type.

Conquer and tackle the smallest subproblems first. Once you’ve figured out a solution that works, use that exact same technique to solve the larger subproblems — in other words, solve the subproblems recursively.

Combine the answers and build up the smaller subproblems until you finally end up applying the same solution to the larger, more complicated problem that you started off with!

The crux of divide and conquer algorithms stems from the fact that it’s a lot easier to solve a complicated problem if you can figure out how to split it up into smaller pieces. By breaking down a problem into its individual parts, the problem becomes a whole lot easier to solve. And usually, once you figure out how to solve a “subproblem”, then you can apply that exact solution to the larger problem. This methodology is exactly what makes recursion the tool of choice for divide-and-conquer algorithms, and it’s the very reason that merge sort is a great example of recursive solutions.

A mergeSort function ultimately has two functions inside of it:

a merge function, which actually combines two lists together and sorts them in the correct order.

a mergeSort function, which will continue to split the input array again and again, recursively, and will also call merge again and again, recursively.

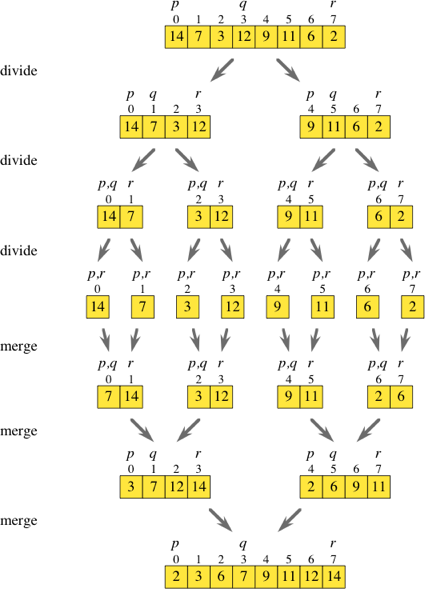
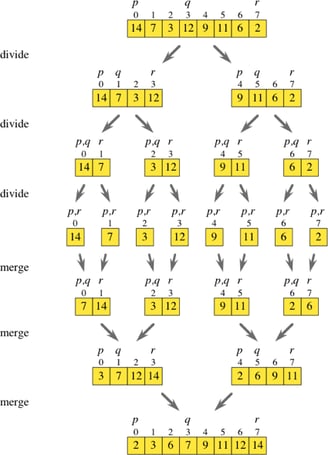
Here is the merge sort pseudocode:
Merge(A, B):
1 - i = 1; j = 1; k = 1;
2 - a_(m+1) = ∞; b_{n+1} = ∞
3 - while (k <= m+n) do:
4 - if (a_i < b_j) then
5 - c_k = a_i; i++;
6 - else
7 - c_k = b_j; j++;
8 - k++;
9 - return C = {c_1, c_2, …, c_(m+n)}
MergeSort(X, n)
1 - if (n == 1) return X
2 - middle = n/2 (round down)
3 - A = {x_1, x_2, …, x_middle}
4 - B = {x_(middle+1), x_{middle+2), …, x_n}
5 - As = MergeSort(A, middle)
6 - Bs = MergeSort(B, n - middle)
7 - return Merge(As, Bs)Indeed, it is because merge sort is implemented recursively that makes it faster than the other algorithms we’ve looked at thus far. Merge sort has O(n log n) running time.


Convex Hull
Given a set of points in the plane. the convex hull of the set is the smallest convex polygon that contains all the points of it.

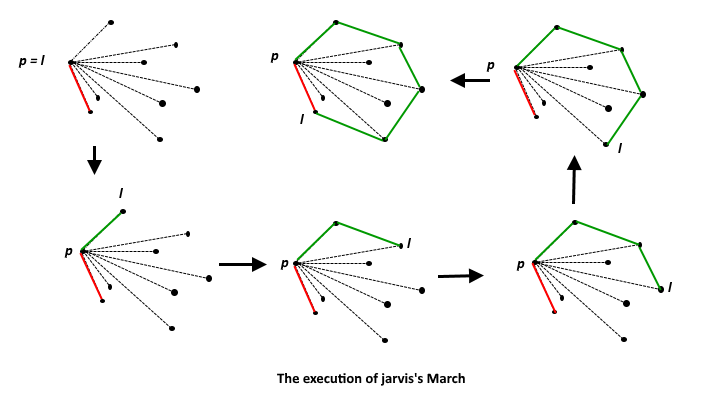
Approach 1 — Gift Wrapping O(n²)
The idea is simple, we start from the leftmost point (or point with minimum x coordinate value) and we keep wrapping points in a counterclockwise direction. Given a point p as the current point, the next point is selected as the point that beats all other points at counterclockwise orientation. Following is the pseudocode:
1 - ConvexHull = Empty list
2 - Find point of smallest x and let it be u (:= u_original)
3 - Let L be the vertical line going through u
3 - Do:
4 - Let v be the point with the smallest angle between L and u * v
5 - Add v to ConvexHull
6 - Let L = uv line
7 - u := v
8 - Until v = u_original
9 - Output ConvexHull

Approach 2 — Graham Scan O(n log n)
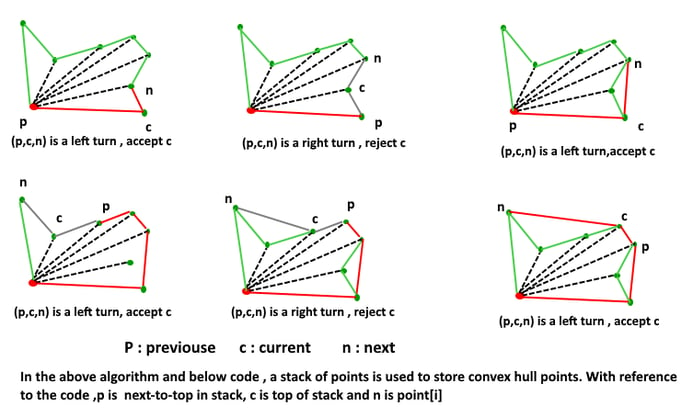
This algorithm can be divided into 2 phases:

• Phase 1 (Sort points): We first find the bottom-most point. The idea is to pre-process points be sorting them with respect to the bottom-most point. Once the points are sorted, they form a simple closed path. What should be the sorting criteria? Computation of actual angles would be inefficient since trigonometric functions are not simple to evaluate. The idea is to use the orientation to compare angles without actually computing them.

• Phase 2 (Accept or Reject Points): Once we have the closed path, the next step is to traverse the path and remove concave points on this path. The first two points in the sorted array are always part of Convex Hull. For remaining points, we keep track of recent three points and find the angle formed by them. Let the three points be prev(p), curr(c) and next(n). If the orientation of these points (considering them in same order) is not counterclockwise, we discard c, otherwise, we keep it.

1 - ConvexHull = Empty list
2 - Let u be the point with smallest x (if more such points, choose the one with smallest y)
3 - Sort the remaining points by by polor angle in counterclockwise order around u
4 - Add u and point 1 to ConvexHull
5 - For i = 2 to n - 1:
6 - While angle of the 2nd-to-last point, last point and i > 180 degree:
7 - Remove last point from ConvexHull
8 - Add i to ConvexHull
9 - Return ConvexHull

Divide and Conquer Algorithms

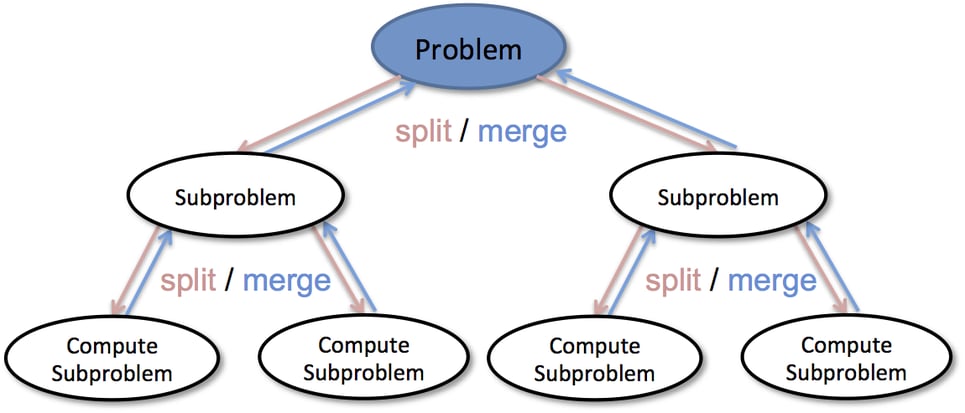
Divide-and-Conquer Algorithm

A very popular algorithmic paradigm, a typical Divide and Conquer algorithm solves a problem using following three steps:

• Divide: Break the given problem into subproblems of same type.

• Conquer: Recursively solve these subproblems

• Combine: Appropriately combine the answers

Following are some standard algorithms that are Divide and Conquer algorithms:
1 — Binary Search is a searching algorithm. In each step, the algorithm compares the input element x with the value of the middle element in array. If the values match, return the index of middle. Otherwise, if x is less than the middle element, then the algorithm recurs for left side of middle element, else recurs for right side of middle element.
2 — Quicksort is a sorting algorithm. The algorithm picks a pivot element, rearranges the array elements in such a way that all elements smaller than the picked pivot element move to left side of pivot, and all greater elements move to right side. Finally, the algorithm recursively sorts the subarrays on left and right of pivot element.
3 — Merge Sort is also a sorting algorithm. The algorithm divides the array in two halves, recursively sorts them and finally merges the two sorted halves.
4 — Closest Pair of Points: The problem is to find the closest pair of points in a set of points in x-y plane. The problem can be solved in O(n²) time by calculating distances of every pair of points and comparing the distances to find the minimum. The Divide and Conquer algorithm solves the problem in O(nLogn) time.
5 — Strassen’s Algorithm is an efficient algorithm to multiply two matrices. A simple method to multiply two matrices need 3 nested loops and is O(n³). Strassen’s algorithm multiplies two matrices in O(n².8974) time.
6 — Cooley–Tukey Fast Fourier Transform (FFT) algorithm is the most common algorithm for FFT. It is a divide and conquer algorithm which works in O(nlogn) time.
7 — Karatsuba algorithm for fast multiplication: It does multiplication of two n-digit numbers in at most 3n^(log 3) single-digit multiplications in general (and exactly n^(log3) when n is a power of 2). It is therefore faster than the classical algorithm, which requires n² single-digit products.
Counting Inversions ProblemWe will consider a problem that arises in the analysis of rankings, which are becoming important to a number of current applications. For example, a number of sites on the Web make use of a technique known as collaborative filtering, in which they try to match your preferences (for books, movies, restaurants) with those of other people out on the Internet. Once the Web site has identified people with “similar” tastes to yours — based on a comparison of how you and they rate various things — it can recommend new things that these other people have liked. Another application arises in recta-search tools on the Web, which execute the same query on many different search engines and then try to synthesize the results by looking for similarities and differences among the various rankings that the search engines return.
A core issue in applications like this is the problem of comparing two rankings. You rank a set of rt movies, and then a collaborative filtering system consults its database to look for other people who had “similar” rankings. But what’s a good way to measure, numerically, how similar two people’s rankings are? Clearly an identical ranking is very similar, and a completely reversed ranking is very different; we want something that interpolates through the middle region.
Let’s consider comparing your ranking and a stranger’s ranking of the same set of n movies. A natural method would be to label the movies from 1 to n according to your ranking, then order these labels according to the stranger’s ranking, and see how many pairs are “out of order.” More concretely, we will consider the following problem. We are given a sequence of n numbers a1, …, an; we will assume that all the numbers are distinct. We want to define a measure that tells us how far this list is from being in ascending order; the value of the measure should be 0 if a1 < a2 < … < an, and should increase as the numbers become more scrambled.
A natural way to quantify this notion is by counting the number of inversions. We say that two indices i < j form an inversion if ai > aj, that is, if the two elements ai and aj are “out of order.” We will seek to determine the number of inversions in the sequence a1, …, an.

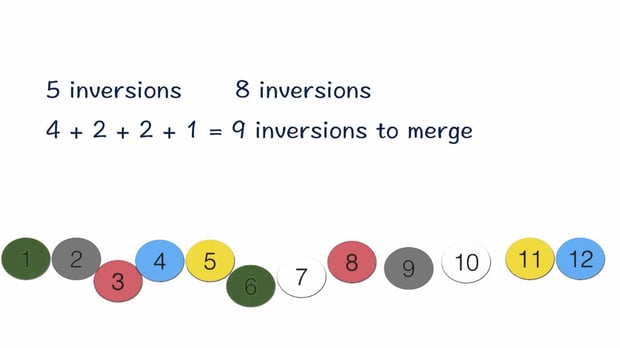
Here’s a pseudocode for a O(n log n) running time algorithm:
Merge-and-Count(A,B)
1 - Maintain a Current pointer into each list, initialized to point to the front elements.
2 - Maintain a variable Count for the number of inversions, initialized to 0.
3 - While both lists are nonempty:
4 - Let a_{i} and b_{j} be the elements pointed to by the Current pointer.
5 - Append the smaller of these two to the output list.
6 - If b_{j} is the smaller element then:
7 - Increment Count by the number of elements remaining in A.
8 - Endif:
9 - Advance the Current pointer in the list from which the smaller element was selected.
10 - EndWhile
11 - Once one list is empty, append the remainder of the other list to the output.
12 - Return Count and the merged list.The running time of Merge-and-Count can be bounded by the analogue of the argument we used for the original merging algorithm at the heart of Mergesort: each iteration of the While loop takes constant time, and in each iteration we add some element to the output that will never be seen again. Thus the number of iterations can be at most the sum of the initial lengths of A and B, and so the total running time is O(n).
We use this Merge-and-Count routine in a recursive procedure that simultaneously sorts and counts the number of inversions in a list L.
Sort-and-Count (L)
1 - If the list has one element, then there are no inversions.
2 - Else:
3 - Divide the list into two halves:
4 - A contains the first [n/2] elements.
5 - B contains the remaining [n/2] elements.
6 - (rA, A) = Sort-and-Count (A).
7 - (rB, B) = Sort-and-Count (B).
8 - (r, L) = Merge-and-Count (A, B).
9 - Endif
10 - Return r = rA + rB + r, and the sorted list L.Since Merge-and-Count takes O(n) time, the running time of Sort-and-Count is O(n log n) for a list with n elements.

Multiplication of Long Numbers Problem

The problem we consider is an extremely basic one: the multiplication of two integers. In a sense, this problem is so basic that one may not initially think of it even as an algorithmic question. But, in fact, elementary schoolers are taught a concrete (and quite efficient) algorithm to multiply two n-digit numbers x and y. You first compute a “partial product” by multiplying each digit of y separately by x, and then you add up all the partial products. Counting a single operation on a pair of bits as one primitive step in this computation, it takes O(n) time to compute each partial product, and O(n) time to combine it in with the running sum of all partial products so far. Since there are n partial products, this is a total running time of O(n²).
If you haven’t thought about this much since elementary school, there’s something initially striking about the prospect of improving on this algorithm. Aren’t all those partial products “necessary” in some way? But, in fact, it is possible to improve on O(n²) time using a different, recursive way of performing the multiplication.

Recursive-Multiply (x, y)

1 - Write x = x_{1} 2^(n/2) + x_{0} and y = y_{1} 2^(n/2) + y_{0}

2 - Compute x_{1} + x_{0} and y_{1} + y_{0}

3 - p = Recursive-Multiply(x_{1} + x_{0}, y_{1} + y_{0})

4 - x_{1} * y_{1} = Recursive-Multiply(x_{1}, y_{1})

5 - x_{0} * y_{0} = Recursive-Multiply(x_{0}, y_{0})

6 - Return x_{1} y_{1} 2^n + (p — x_{1} y_{1} — x_{0} y_{0}) 2^(n/2) + x_{0} y_{0}We can determine the running time of this algorithm as follows. Given two n-bit numbers, it performs a constant number of additions on O(n)-bit numbers, in addition to the three recursive calls. Ignoring for now the issue that x_{1} + x_{0} and y_{1} + y_{0} may have n / 2 + 1 bits (rather than just n/2), which turns out not to affect the asymptotic results, each of these recursive calls is on an instance of size n/2. Thus, in place of our four-way branching recursion, we now have a three-way branching one, with a running time that satisfies T(n) <_ 3T(n/2) + cn for a constant c. This is case 3 of the Master Theorem describes below, which gives the running time of O(n^1.59).

The master theorem provides a solution to recurrence relations of the form:

for constants a >= 1 and b > 1 with f asymptotically positive. Such recurrences occur frequently in the runtime analysis of many commonly encountered algorithms. The following statements are true:

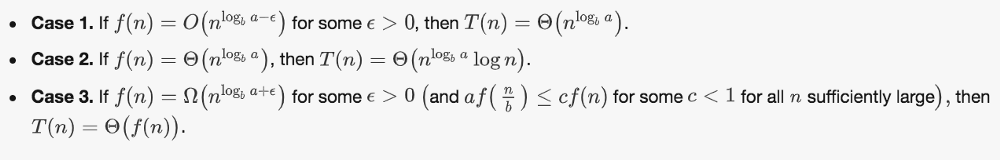
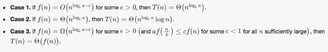
Sources:

• Divide and Conquer Algorithm — Introduction (GeeksforGeeks)

• Master Theorem (Brilliant)

• Counting Inversion (Chula Engineering)

• Karatsuba Algorithm (Brilliant)

Greedy Algorithms and Dynamic Programming

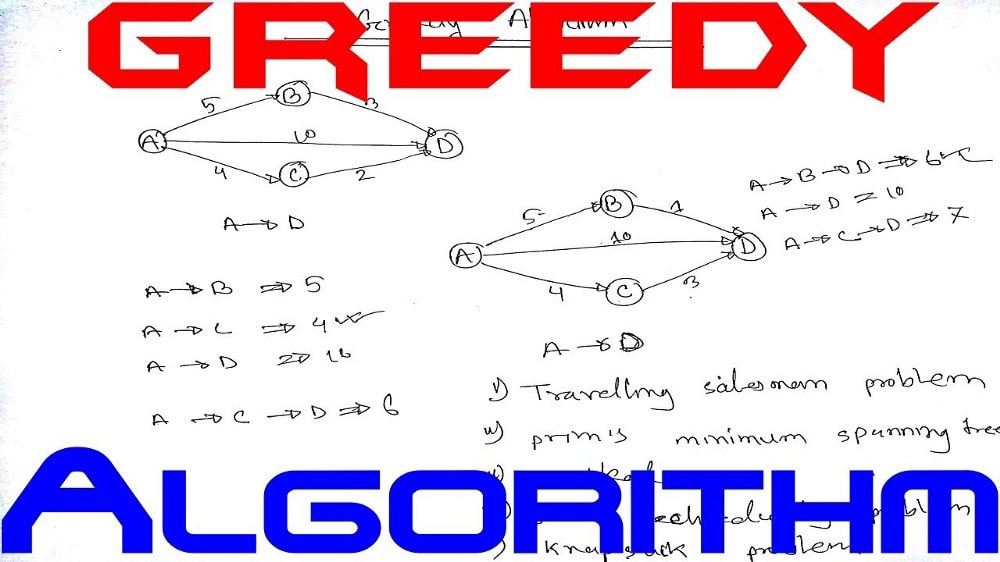
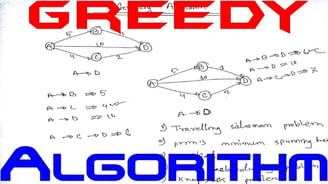
In an algorithm design, there is no one ‘silver bullet’ that is a cure for all computation problems. Different problems require the use of different kinds of techniques. A good programmer uses all these techniques based on the type of problem. In this blog post, I am going to cover 2 fundamental algorithm design principles:

greedy algorithms and dynamic programming.

Greedy Algorithm

A greedy algorithm, as the name suggests, always makes the choice that seems to be the best at that moment. This means that it makes a locally-optimal choice in the hope that this choice will lead to a globally-optimal solution.
How do you decide which choice is optimal?
Assume that you have an objective function that needs to be optimized (either maximized or minimized) at a given point. A Greedy algorithm makes greedy choices at each step to ensure that the objective function is optimized. The Greedy algorithm has only one shot to compute the optimal solution so that it never goes back and reverses the decision.
Greedy algorithms have some advantages and disadvantages:

1. It is quite easy to come up with a greedy algorithm (or even multiple greedy algorithms) for a problem.

2. Analyzing the run time for greedy algorithms will generally be much easier than for other techniques (like Divide and conquer). For the Divide and conquer technique, it is not clear whether the technique is fast or slow. This is because at each level of recursion the size of gets smaller and the number of sub-problems increases.

3. The difficult part is that for greedy algorithms you have to work much harder to understand correctness issues. Even with the correct algorithm, it is hard to prove why it is correct. Proving that a greedy algorithm is correct is more of an art than a science. It involves a lot of creativity.

Dynamic Programming

Let us say that we have a machine, and to determine its state at time t, we have certain quantities called state variables. There will be certain times when we have to make a decision which affects the state of the system, which may or may not be known to us in advance. These decisions or changes are equivalent to transformations of state variables. The results of the previous decisions help us in choosing the future ones.
What do we conclude from this? We need to break up a problem into a series of overlapping sub-problems, and build up solutions to larger and larger sub-problems. If you are given a problem, which can be broken down into smaller sub-problems, and these smaller sub-problems can still be broken into smaller ones — and if you manage to find out that there are some over-lappping sub-problems, then you’ve encountered a DP problem.
The core idea of Dynamic Programming is to avoid repeated work by remembering partial results and this concept finds it application in a lot of real life situations.
In programming, Dynamic Programming is a powerful technique that allows one to solve different types of problems in time O(n2) or O(n3) for which a naive approach would take exponential time.

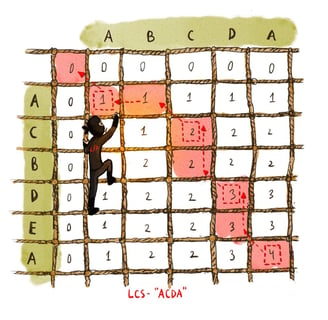
Let’s go over a couple of well-known optimization problems that use either of these algorithmic design approaches:

1 — Basic Interval Scheduling Problem
In this problem, our input is a set of time-intervals and our output is a subset of non-overlapping intervals. Our objective is to maximize the number of selected intervals in a given timeframe. The greedy approach is to consider jobs in increasing order of finish time, and then teak each job provided it’s compatible with the ones already taken. Here’s the O(n²) implementation pseudocode:
Interval-Scheduling( (s_{1}, f_{1}), …, (s_{n}, f_{n}) ):
1 - Remain = {1, …, n}
2 - Selected = {}
3 - While (|Remain| > 0) {
4 - k in Remain is such that f_{k} = min of f_{i} (i in Remain)
5 - Selected = Selected and {k}
6 - Remain = Remain - {k}
7 - for every i in Remain {
8 - if (s_{i} < f_{k} then Remain = Remain - {i}
9 - }
10 - }
11 - return Selected
This greedy algorithm is optimal, but we can also use dynamic programming to solve this problem. After sorting the interval by finishing time, we let S[k] = max(S[k — 1], 1 + S[j]):

• Where k represents the intervals order by finish time.

• Where j < k is the largest index such that the finish time of item j does not overlap the start time of item k.

• 
  

2 — Scheduling All Intervals Problem
In this problem, our input is a set of time-intervals and our output is a partition of the intervals, each part of the partition consists of non-overlapping intervals. Our objective is to minimize the number of parts in the partition. The greedy approach is to consider intervals in increasing order of start time and then assign them to any compatible part. Here’s the O(n logn) implementation pseudocode:
Schedule-All-Intervals((s_{0},f_{0}), …, (s_{n-1},f_{n-1})):
1 - Sort intervals by their starting time.
2 - For j = 0 to n - 1 do:
3 - Consider = {1, …, depth}
4 - For every i < j that overlaps with j do:
5 - Consider = Consider - { Label[i] }
6 - If |Consider| > 0 then:
7 - Label[j] = anything from Consider
8 - Else:
9 - Label[j] = nothing
10 - Return Label[]The algorithm is optimal and it never schedules two incompatible intervals in the same parts.

3 — Weight Interval Scheduling Problem
In this problem, our input is a set of time-intervals, where each interval has a cost. Our output is a subset of non-overlapping intervals. Our objective is to maximize the sum of the costs in the subset. A simple brute force approach can be viewed below:
Weighted-Scheduling-Attempt ((s_{1}, f_{1}, c_{1}), …, (s_{n}, f_{n}, c_{n})):
1 - Sort intervals by their finish time.
2 - Return Weighted-Scheduling-Recursive (n)
Weighted-Scheduling-Recursive (j):
1 - If (j = 0) then Return 0
2 - k = j
3 - While (interval k and j overlap) do k—-
4 - Return max(c_{j} + Weighted-Scheduling-Recursive (k), Weighted-Scheduling-Recursive (j - 1))Although this approach works, it fails spectacularly because of redundant sub-problems, which leads to exponential running time. To improve time complexity, we can try a top-down dynamic programming method known as memoization. Below you can see an O(n²) pseudocode:
Weighted-Sched ((s_{1}, f_{1}, c_{1}), …, (s_{n}, f_{n}, c_{n})):
1 - Sort intervals by their finish time.
2 - Define S[0] = 0
3 - For j = 1 to n do:
4 - k = j
5 - While (intervals k and j overlap) do k—-
6 - S[j] = max(S[j - 1], c_{j} + S[k])
7 - Return S[n]

4 — Longest Increasing Subsequence Problem
For this problem given an input as a sequence of numbers, we want an output of an increasing subsequence. Our goal is to maximize the length of that subsequence. Using dynamic programming again, an O(n²) algorithm follows:
Longest-Incr-Subseq(a_{1}, …, a_{n}):
1 - For j = 1 to n do:
2 - S[j] = 1
3 - For k = 1 to j - 1 do:
4 - If a_{k} < a_{j} and S[j] < S[k] + 1 then:
5 - S[j] = S[k] + 1
6 - Return max_{j} S[j]S[j] is the maximum length of an increasing subsequence of the first j numbers ending with the j-th. Note that S[j] = 1 + maximum S[k] where k < j and a_{k} < a_{j}.


Comparison
We can make whatever choice seems best at the moment and then solve the subproblems that arise later. The choice made by a greedy algorithm may depend on choices made so far but not on future choices or all the solutions to the subproblem. It iteratively makes one greedy choice after another, reducing each given problem into a smaller one. In other words, a greedy algorithm never reconsiders its choices.
This is the main difference from dynamic programming, which is exhaustive and is guaranteed to find the solution. After every stage, dynamic programming makes decisions based on all the decisions made in the previous stage, and may reconsider the previous stage’s algorithmic path to solution.
For example, let’s say that you have to get from point A to point B as fast as possible, in a given city, during rush hour. A dynamic programming algorithm will look into the entire traffic report, looking into all possible combinations of roads you might take, and will only then tell you which way is the fastest. Of course, you might have to wait for a while until the algorithm finishes, and only then you can start driving. The path you will take will be the fastest one (assuming that nothing changed in the external environment).
On the other hand, a greedy algorithm will start you driving immediately and will pick the road that looks the fastest at every intersection. As you can imagine, this strategy might not lead to the fastest arrival time, since you might take some “easy” streets and then find yourself hopelessly stuck in a traffic jam.

50+ Data Structure,Algorithms & Programming Languages Interview Questions for Programmers

There are a lot of computer science graduates and programmers applying for programming, coding, and software development roles at startups like Uber and Netflix; big organizations like Amazon, Microsoft, and Google; and service-based companies like Infosys or Luxsoft, but many of them have no idea of what kind of programming interview questions to expect when you're applying for a job with these companies.
In this article, I'll share some frequently asked programming interview questions from different interviews for programmers at different levels of experience, from people who have just graduated from college to programmers with one to two years of experience.
Coding interviews are comprised mainly of data structure and algorithm-based questions as well as some of the logical questions such as, How do you swap two integers without using a temporary variable?
I think it's helpful to divide coding interview questions into different topic areas. The topic areas I've seen most often in interviews are array, linked list, string, binary tree, as well as questions from algorithms (e.g. string algorithm, sorting algorithms like quicksort or radix sort, and other miscellaneous ones), and that's what you will find in this article.

It's not guaranteed that you will be asked these coding or data structure and algorithmic questions

but they will give you enough of an idea of the kinds of questions you can expect in a real programming job interview.
Once you have gone through these questions, you should feel confident enough to attend any telephonic or face-to-face interviews.
Btw, there is no point in attempting these questions if you don't have sufficient knowledge of essential Data Structure and Algorithms or you have not touched them from ages.
In that case, you should take a good course like Algorithms and Data Structures Part 1 and 2 By Robert Horvick to refresh your DS and algorithms skills.
Top 50 Algorithms and Coding Interview Questions
Without any further ado, here is my list of some of the most frequently asked coding interview questions from programming job interviews:
1. Array Coding Interview Questions
An array is the most fundamental data structure, which stores elements at a contiguous memory location. It is also one of the darling topics of interviewers and you will hear a lot of questions about an array in any coding interview, e.g. reversing an array, sorting the array, or searching elements on the array.
The key benefit of an array data structure is that it offers fast O(1) search if you know the index, but adding and removing an element from an array is slow because you cannot change the size of the array once it's created.
In order to create a shorter or longer array, you need to create a new array and copy all elements from old to new.
The key to solving array-based questions is having a good knowledge of array data structure as well as basic programming constructors such as loop, recursion, and fundamental operators.
Here are some of the popular array-based coding interview questions for your practice:

1. How do you find the missing number in a given integer array of 1 to 100? (solution)

2. How do you find the duplicate number on a given integer array? (solution)

3. How do you find the largest and smallest number in an unsorted integer array? (solution)

4. How do you find all pairs of an integer array whose sum is equal to a given number? (solution)

5. How do you find duplicate numbers in an array if it contains multiple duplicates? (solution)

6. How are duplicates removed from a given array in Java? (solution)

7. How is an integer array sorted in place using the quicksort algorithm? (solution)

8. How do you remove duplicates from an array in place? (solution)

9. How do you reverse an array in place in Java? (solution)

10. How are duplicates removed from an array without using any library? (solution)

These questions will not only help you to develop your problem-solving skills but also improve your knowledge of array data structure.
If you need more advanced questions based upon array then you can see also seeThe Coding Interview Bootcamp: Algorithms + Data Structures, a boot camp style course on algorithms, especially designed for interview preparation to get a job on technical giants like Google, Microsoft, Apple, Facebook etc.
And, if you feel 10 is not enough questions and you need more practice, then you can also check out this list of 30 array questions.
2. Linked List Programming Interview Questions
A linked list is another common data structure that complements the array data structure. Similar to the array, it is also a linear data structure and stores elements in a linear fashion.
However, unlike the array, it doesn't store them in contiguous locations; instead, they are scattered everywhere in memory, which is connected to each other using nodes.
A linked list is nothing but a list of nodes where each node contains the value stored and the address of the next node.
Because of this structure, it's easy to add and remove elements in a linked list, as you just need to change the link instead of creating the array, but the search is difficult and often requires O(n) time to find an element in the singly linked list.
This article provides more information on the difference between an array and linked list data structures.
It also comes in varieties like a singly linked list, which allows you to traverse in one direction (forward or reverse); a doubly linked list, which allows you to traverse in both directions (forward and backward); and finally, the circular linked list, which forms a circle.
In order to solve linked list-based questions, a good knowledge of recursion is important, because a linked list is a recursive data structure.
If you take one node from a linked list, the remaining data structure is still a linked list, and because of that, many linked list problems have simpler recursive solutions than iterative ones.
Here are some of the most common and popular linked list interview questions and their solutions:

1. How do you find the middle element of a singly linked list in one pass? (solution)

2. How do you check if a given linked list contains a cycle? How do you find the starting node of the cycle? (solution)

3. How do you reverse a linked list? (solution)

4. How do you reverse a singly linked list without recursion? (solution)

5. How are duplicate nodes removed in an unsorted linked list? (solution)

6. How do you find the length of a singly linked list? (solution)

7. How do you find the third node from the end in a singly linked list? (solution)

8. How do you find the sum of two linked lists using Stack? (solution)

These questions will help you to develop your problem-solving skills as well as improve your knowledge of the linked list data structure.
If you are having trouble solving these linked list coding questions then I suggest you refresh your data structure and algorithms skill by going through Data Structures and Algorithms: Deep Dive Using Java course.
You can also check out this list of 30 linked list interview questions for more practice questions.

3. String Coding Interview Questions
Along with array and linked list data structures, a string is another popular topic on programming job interviews. I have never participated in a coding interview where no string-based questions were asked.
A good thing about the string is that if you know the array, you can solve string-based questions easily because strings are nothing but a character array.
So all the techniques you learn by solving array-based coding questions can be used to solve string programming questions as well.
Here is my list of frequently asked string coding questions from programming job interviews:

1. How do you print duplicate characters from a string? (solution)

2. How do you check if two strings are anagrams of each other? (solution)

3. How do you print the first non-repeated character from a string? (solution)

4. How can a given string be reversed using recursion? (solution)

5. How do you check if a string contains only digits? (solution)

6. How are duplicate characters found in a string? (solution)

7. How do you count a number of vowels and consonants in a given string? (solution)

8. How do you count the occurrence of a given character in a string? (solution)

9. How do you find all permutations of a string? (solution)

10. How do you reverse words in a given sentence without using any library method? (solution)

11. How do you check if two strings are a rotation of each other? (solution)

12. How do you check if a given string is a palindrome? (solution)

These questions help improve your knowledge of string as a data structure. If you can solve all these String questions without any help then you are in good shape.
For more advanced questions, I suggest you solve problems given in the Algorithm Design Manual by Steven Skiena, a book with the toughest algorithm questions.
If you need more practice, here is another list of 20 string coding questions.
4. Binary Tree Coding Interview Questions
So far, we have looked at only the linear data structure, but all information in the real world cannot be represented in linear fashion, and that's where tree data structure helps.
Tree data structure is a data structure that allows you to store your data in a hierarchical fashion. Depending on how you store data, there are different types of trees, such as a binary tree, where each node has, at most, two child nodes.a
Along with its close cousin binary search tree, it's also one of the most popular tree data structures. Therefore, you will find a lot of questions based on them, such as how to traverse them, count nodes, find depth, and check if they are balanced or not.
A key point to solving binary tree questions is a strong knowledge of theory, e.g. what is the size or depth of the binary tree, what is a leaf, and what is a node, as well as an understanding of the popular traversing algorithms, e.g. pre-, post-, and in-order traversal.
Here is a list of popular binary tree-based coding questions from software engineer or developer job interviews:

• How is a binary search tree implemented? (solution)

• How do you perform preorder traversal in a given binary tree? (solution)

• How do you traverse a given binary tree in preorder without recursion? (solution)

• How do you perform an inorder traversal in a given binary tree? (solution)

• How do you print all nodes of a given binary tree using inorder traversal without recursion? (solution)

• How do you implement a postorder traversal algorithm? (solution)

• How do you traverse a binary tree in postorder traversal without recursion? (solution)

• How are all leaves of a binary search tree printed? (solution)

• How do you count a number of leaf nodes in a given binary tree? (solution)

• How do you perform a binary search in a given array? (solution)

If you feel that your understanding of binary tree coding is inadequate and you can't solve these questions on your own, I suggest you go back and pick a good data structure and algorithm course like From 0 to 1: Data Structures & Algorithms in Java.
If you need some more recommendations, here is my list of useful data structure algorithm books and courses to start with.
5. Miscellaneous Coding Interview Questions
Apart from data structure-based questions, most of the programming job interviews also ask algorithm, design, bit manipulation, and general logic-based questions, which I'll describe in this section.
It's important that you practice these concepts because sometimes they become tricky to solve in the actual interview. Having practiced them before not only makes you familiar with them but also gives you more confidence in explaining the solution to the interviewer.

• How is a bubble sort algorithm implemented? (solution)

• How is an iterative quicksort algorithm implemented? (solution)

• How do you implement an insertion sort algorithm? (solution)

• How is a merge sort algorithm implemented? (solution)

• How do you implement a bucket sort algorithm? (solution)

• How do you implement a counting sort algorithm? (solution)

• How is a radix sort algorithm implemented? (solution)

• How do you swap two numbers without using the third variable? (solution)

• How do you check if two rectangles overlap with each other? (solution)

• How do you design a vending machine? (solution)

If you need more such coding questions you can take help from books like Cracking The Code Interview, by Gayle Laakmann McDowell which presents 189+ Programming questions and solution. A good book to prepare for programming job interviews in a short time.
By the way, the more questions you solve in practice, the better your preparation will be. So, if you think 50 is not enough and you need more, then check out these additional 50 programming questions for telephone interviews and these books and courses for a more thorough preparation.
Now You're Ready for the Coding Interview
These are some of the most common questions outside of data structure and algorithms that help you to do really well in your interview.
I have also shared a lot of these questions on my blog, so if you are really interested, you can always go there and search for them.
These common coding, data structure, and algorithm questions are the ones you need to know to successfully interview with any company, big or small, for any level of programming job.
If you are looking for a programming or software development job in 2018, you can start your preparation with this list of coding questions.
This list provides good topics to prepare and also helps assess your preparation to find out your areas of strength and weakness.
A good knowledge of data structure and algorithms is important for success in coding interviews and that's where you should focus most of your attention.